Введение
Данный проект является пробой пера в управлении шестиногим роботом "Лапчик". Весь исходный код проекта можно найти в публичном репозитории [1].

Схема управления
Для движения робота для каждой лапки определяется желаемое текущее положение в зависимости от траектории движения и текущей фазы циклограммы соответствующей лапки. В дальнейшем этот угол отрабатывается шестью локальными П-ПИ регуляторами (по одному на каждую лапку).
Лапки объеденены в два так называемых "трипода":
| L | R |
|---|---|
R |
L |
L |
R |
Лапки внутри одного трипода синхронизированы и отрабатывают заранее заданный профиль движения.
Профиль движения левого и правого трипода отличаются по фазе на 180o.
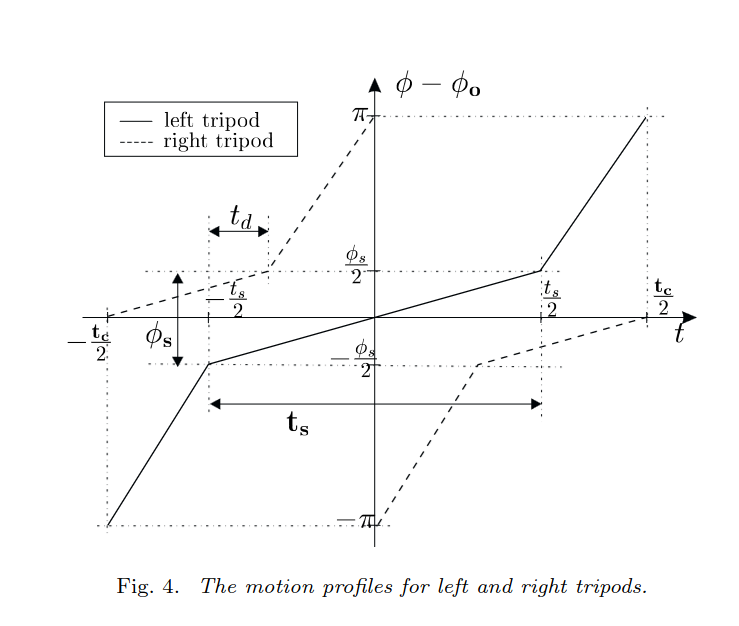
Профиль лапки характеризуется параметрической функцией
Функция представляет из себя кусочно-линейную и связывает текущую фазу внутри циклограммы с требуемым углом лапки.
Математическое описание этой функции можно получить в [3].
Реализация в коде приведена ниже:
#pragma once
#include <FixMath.h>
#define LOG(x) String(x) + " " +
typedef float sfix;
const auto tc = (sfix(2*M_PI));
const auto ts (sfix(2*2/3.6*M_PI));
const auto phis (sfix(1.5));
const auto phi0 (sfix(-2));
sfix modc(sfix in, sfix modder)
{
in = in + modder;
while(in > modder*sfix(0.5))
{
in = in - modder;
}
return in;
}
inline sfix Fc(sfix t, sfix phists)
{
return t*phists;
}
inline sfix Fr0(sfix t, sfix dydx)
{
return t*dydx;
}
inline sfix Fcomp(sfix ts, sfix phists, sfix dydx)
{
return Fc(ts*sfix(0.5), phists) - Fr0(ts*sfix(0.5), dydx);
}
inline sfix Fr(sfix t, sfix ts, sfix phists, sfix dydx)
{
return Fr0(t, dydx) + Fcomp(ts, phists, dydx);
}
inline sfix Fl(sfix t, sfix ts, sfix phists, sfix dydx)
{
return -Fr(-t, ts, phists, dydx);
}
inline sfix Ffull(sfix t, sfix tc, sfix ts, sfix phis, sfix phi0)
{
t = modc(t, tc);
sfix out;
auto phists = phis/ts;
if(t < -ts*sfix(0.5))
{
auto dydx = (sfix(2*M_PI) - phis) / (tc - ts);
out = Fl(t, ts, phists, dydx);
}
else if(t < ts*sfix(0.5))
{
out = Fc(t, phists);
}
else
{
auto dydx = (sfix(2*M_PI) - phis) / (tc - ts);
out = Fr(t, ts, phists, dydx);
}
return out + phi0;
}Для управления углом каждой лапки была использована экспериментальная библиотека ALFA4C [2], вдохновляющаяся языком программирования реактивных систем ALFA [5].
Исходный код приведен ниже:
#pragma once
#include "RHex.h"
#include "alfa4c.h"
#include "Defines.h"
extern sfix forward_vel;
extern sfix ang_vel;
ChannelSensor<sfix> forward_velocity_command_raw(&forward_vel), angular_velocity_command(&ang_vel);
ChannelComputed<sfix> forward_velocity_command([](){ return -forward_velocity_command_raw; });
ChannelLast<sfix> leg_phase, leg_phase_delta;
ChannelLast<sfix> leg_angles[6], leg_angles_smoothed[6];
MODULE(update_forw_phase,
DRIVE(leg_phase, modc(leg_phase.get() + forward_velocity_command.get() * sfix(Ts_s), sfix(2*M_PI)))
)
MODULE(update_delta_phase,
DRIVE(leg_phase_delta, modc(leg_phase_delta.get() + angular_velocity_command.get() * sfix(Ts_s), sfix(2*M_PI)))
)
MODULE(stand_up,
for(size_t i = 0; i < 6; i++)
{
// DRIVE(leg_angles[i], phi0 + M_PI * (i%2))
DRIVE(leg_angles[i], leg_angles[i] + constrain((phi0+ M_PI * (i%2) - leg_angles[i]), -2, 2)*Ts_s)
}
Serial.println("Standup");
// DRIVE(leg_angles[1], )
// DRIVE(leg_angles[2], )
// DRIVE(leg_angles[3], )
// DRIVE(leg_angles[4], )
// DRIVE(leg_angles[5], )
)
MODULE(move_forward,
DRIVE(leg_angles[0], modc(Ffull(leg_phase, tc, ts, phis, phi0), sfix(2*M_PI)))
DRIVE(leg_angles[1], modc(Ffull(leg_phase.get() + sfix(M_PI), tc, ts, phis, phi0), sfix(2*M_PI)))
DRIVE(leg_angles[2], modc(Ffull(leg_phase, tc, ts, phis, phi0), sfix(2*M_PI)))
DRIVE(leg_angles[3], modc(Ffull(leg_phase.get() + sfix(M_PI), tc, ts, phis, phi0), sfix(2*M_PI)))
DRIVE(leg_angles[4], modc(Ffull(leg_phase, tc, ts, phis, phi0), sfix(2*M_PI)))
DRIVE(leg_angles[5], modc(Ffull(leg_phase.get() + sfix(M_PI), tc, ts, phis, phi0), sfix(2*M_PI)))
Serial.println("Forward");
)
MODULE(rotate_in_place,
DRIVE(leg_angles[0], modc(Ffull(leg_phase + leg_phase_delta, tc, ts, phis, phi0), sfix(2*M_PI)))
DRIVE(leg_angles[1], modc(Ffull(leg_phase + sfix(M_PI) + leg_phase_delta, tc, ts, phis, phi0), sfix(2*M_PI)))
DRIVE(leg_angles[2], modc(Ffull(leg_phase + leg_phase_delta, tc, ts, phis, phi0), sfix(2*M_PI)))
DRIVE(leg_angles[3], modc(Ffull(leg_phase + sfix(M_PI) - leg_phase_delta, tc, ts, phis, phi0), sfix(2*M_PI)))
DRIVE(leg_angles[4], modc(Ffull(leg_phase - leg_phase_delta, tc, ts, phis, phi0), sfix(2*M_PI)))
DRIVE(leg_angles[5], modc(Ffull(leg_phase + sfix(M_PI) - leg_phase_delta, tc, ts, phis, phi0), sfix(2*M_PI)))
)
MODULE(move_soft,
for(size_t i = 0; i < 6; i++)
{
// DRIVE(leg_angles_smoothed[i], leg_angles_smoothed[i] + constrain((leg_angles[i] - leg_angles_smoothed[i]), -2, 2)*Ts_s)
DRIVE(leg_angles_smoothed[i], leg_angles[i])
}
)
Updatable *links[] =
{
¤t_real_time_ms,
&forward_velocity_command_raw,
&forward_velocity_command,
&angular_velocity_command,
&update_forw_phase,
&update_delta_phase,
&leg_phase,
&leg_phase_delta,
// &move_forward,
// &rotate_in_place,
&stand_up,
&leg_angles[0],
&leg_angles[1],
&leg_angles[2],
&leg_angles[3],
&leg_angles[4],
&leg_angles[5],
&move_soft,
&leg_angles_smoothed[0],
&leg_angles_smoothed[1],
&leg_angles_smoothed[2],
&leg_angles_smoothed[3],
&leg_angles_smoothed[4],
&leg_angles_smoothed[5],
};
#define LINK_SIZE (sizeof(links)/sizeof(links[0]))
void select_module(Module *module)
{
links[8] = module;
}
void ALFA_update()
{
for(size_t i = 0; i < LINK_SIZE; i++)
{
links[i]->update();
}
}Для движения вперед основная программа должна выбрать соответствующий модуль move_forward и записать требуемую скорость в глобальную переменную forward_vel.
Источники
[1] "https://github.com/arsenier/PobeditelRTK"
[2] "https://github.com/arsenier/ALFA4C"
[3] "https://www.desmos.com/calculator/nokfdmo4bt"
[4] “https://www.rhex.web.tr/saranli_buehler_koditschek.ijrr2001.pdf.” Accessed: Jun. 08, 2024. [Online]. Available: https://www.rhex.web.tr/saranli_buehler_koditschek.ijrr2001.pdf
[5] E. Gat, “ALFA: a language for programming reactive robotic control systems,” in Proceedings. 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA: IEEE Comput. Soc. Press, 1991, pp. 1116–1121. doi: 10.1109/ROBOT.1991.131743.